Answer:
Van = 18
Bus = 58
Explanation:
Let v be the number of students carried by each van.
Let b be the number of students carried by each bus.
We know the following:
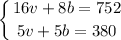
Solve the second equation for b:
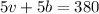
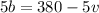
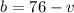
Replace b with (76 – v) in the first equation:
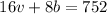
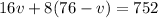
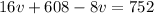
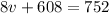
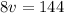
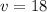
Therefore, each van can carry 18 students. Each bus, then, can carry 76 – v = 76 – 18 = 58.
To verify:
High School A had 16 vans and 8 buses equaling (16 × 18) + (8 × 58) = 288 + 464 = 752. That is correct.
High School B had 5 vans and 5 buses equaling (5 × 18) + (5 × 58) = 90 + 290 = 380. That is correct.