Question

Use the remainder theorem to find the value of F(x).
Find F(3).
F(x) = -x^3+ 4x² – 2x

Answer 1

Using remainder value theorem, the value of f(3) is 3

Solution:

Given, function is
`f(x)=-x^(3)+4 x^(2)-2 x`

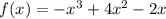
We have to find the value of f(3) by using remainder theorem.

Now, we have to divide f(x) with x – 3, because we want value of f(3)

If we want f(a), then we have to divide with x – a.

Now, first let us factorize the f(x)

`\begin{array}{l}{\text { Then, } f(x)=-x^(3)+4 x^(2)-2 x} \\\\ {=-x\left(x^(2)-4 x+2\right)} \\\\ {=-x\left(x^(2)-4 x+3-1\right)} \\\\ {=-x\left(x^(2)-3 x-x+3-1\right)} \\\\ {=-x(x(x-3)-1(x-3)-1)} \\\\ {=-x((x-3)(x-1)-1)} \\\\ {=-x(x-3)(x-1)+x}\end{array}`

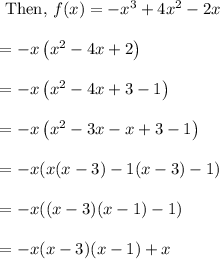
Now, let us divide the f(x) with x – 3

`\begin{array}{l}{\rightarrow \frac{-\mathrm{x}(\mathrm{x}-3)(\mathrm{x}-1)+\mathrm{x}}{x-3}=(-x(x-3)(x-1))/(x-3)+(x)/(x-3)} \\\\ {=-\mathrm{x}(\mathrm{x}-1)+(x-3+3)/(x-3)} \\\\ {=-\mathrm{x}(\mathrm{x}-1)+1+(3)/(x-3)}\end{array}`

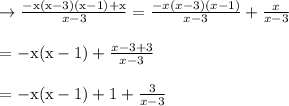
Now, multiply f(x) with (x -3) ⇒ (-x(x -1) + 1)(x -3) + 3

This is in the form of:

`\text {quotient } * \text { divisor }+\text { remainder.}`

Hence, the remainder is 3.

Therefore the value of f(3) is 3