Answer:
24.084 m/s
Step-by-step explanation:
From the law of conservation of linear momentum
Total momentum before collision equals to the total momentum after collision
Since momentum=mv where m is mass and v is velocity
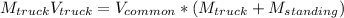 where
where
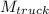 is the mass of the truck,
is the mass of the truck,
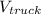 is velocity of the truck,
is velocity of the truck,
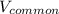 is the common velocity of moving and standing truck after collision and
is the common velocity of moving and standing truck after collision and
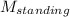 is the mass of the standing truck
is the mass of the standing truck
Making
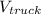 the subject we obtain
the subject we obtain
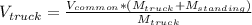
Substituting
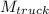 as 25000 Kg,
as 25000 Kg,
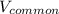 as 22.3 m/s,
as 22.3 m/s,
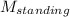 as 2000 Kg we obtain
as 2000 Kg we obtain

Therefore, assuming no friction and considering that after collision they still move eastwards hence common velocity and initial truck velocities are positive
The truck was moving at 24.084 m/s