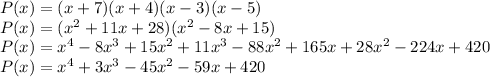Answer:
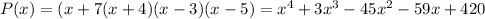
Explanation:
Given:
The zeros of the polynomial are -7, -4, 3 and 5.
The coefficient of
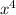 is 1.
is 1.
A polynomial of degree 4 has maximum 4 zeros.
Let the polynomial be
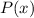 .
.
Since,
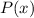 has zeros -7, -4, 3 and 5, therefore,
has zeros -7, -4, 3 and 5, therefore,
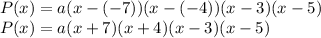
Where,
 is coefficient of
is coefficient of
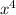 .
.
But, coefficient of
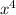 is 1. So,
is 1. So,
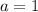
∴