Question

Select all values for y that belong to the solution set of the following compound inequality. −4y + 9 > 37 or 3y − 11 ≥ −17 Select one or more: A. 4 B. 0 C. -2 D. -5 E. 6 F. -13

Answer 1

A. 4

B. 0

C. -2

E. 6

F. -13

Explanation:

step 1

Solve the inequality A

we have

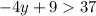`-4y+9 > 37` ----> inequality A

Multiply by -1 both sides

`4y-9 < -37`

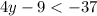
Adds 9 both sides

`4y < -37+9`

`4y < -28`

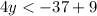
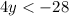
Divide by 4 both sides

`y < -7`

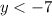
The solution of the inequality A is the interval (-∞,-7)

step 2

Solve the inequality B

we have

`3y-11\geq -17` ----> inequality B

Adds 11 both sides

`3y\geq -17+11`

`3y\geq -6`

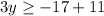
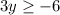
Divide by 3 both sides

`y\geq -2`

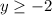
The solution of the inequality B is the interval [-2,∞)

step 3

Find the solution of the system of inequalities

inequality A or inequality B

The solution is

(-∞,-7) ∪ [-2,∞)

If a value of y is a solution of the compound inequality, then the value must lie on any of the two intervals of the solution

Verify all values

case A) 4

The value of y lie on the interval [-2,∞)

therefore

4 belong to the solution set

case B) 0

The value of y lie on the interval [-2,∞)

therefore

0 belong to the solution set

case C) -2

The value of y lie on the interval [-2,∞)

therefore

-2 belong to the solution set

case D) -5

The value of y not lie on the interval (-∞,-7) and not lie on the interval [-2,∞)

therefore

-5 belong to the solution set

case E) 6

The value of y lie on the interval [-2,∞)

therefore

6 belong to the solution set

case F) -13

The value of y lie on the interval (-∞,-7)

therefore

-13 belong to the solution set