Answer:
Relative minima at
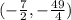 , and relative maxima DNE.
, and relative maxima DNE.
Step-by-step explanation:
The given function is f(x) = x (x + 7) ...... (1)
We have to calculate the relative maxima and relative minima at point (x, y).
Rearranging the function given above we get.
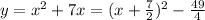
⇒
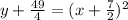
Now, this is an equation of parabola having vertex at
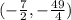 and the axis is parallel to positive Y-axis.
and the axis is parallel to positive Y-axis.
Therefore, the function(1) has a relative minima at
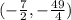 , and the relative maxima DNE. (Answer)
, and the relative maxima DNE. (Answer)