Answer:
A. The maximum heigh is 81 feet
B. The ball will reach the maximum heiight at 2.25 seconds
C. The domain of the function is
![t\in [0,4.5]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4coaqrnra67hvavfzm59zzvt0zxr92g0qy.png)
D. The range of the function is
![h(t)\in [0,81]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qxkuj2pfkmq2uw291pocxxzt3d1pg4t6ce.png)
E. 4.5 seconds
Explanation:
A ball was thrown into the air with an initial velocity of 72 feet per second. The height of the ball after t seconds is represented by the equation:
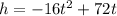
The maximum height will be at parabola's vertex. Find it:
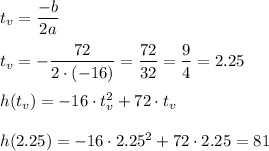
A. The maximum heigh is 81 feet
B. The ball will reach the maximum heiight at 2.25 seconds
C. Find where the parabola intersects the x-axis:
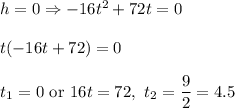
So, the domain of the function is
![t\in [0,4.5]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4coaqrnra67hvavfzm59zzvt0zxr92g0qy.png)
D. The range of the function is
![h(t)\in [0,81]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qxkuj2pfkmq2uw291pocxxzt3d1pg4t6ce.png)
E. The ball is at the air for 4.5 seconds