Question

A unit square and a rectangle have the same perimeter. What is the length of the rectangle if its area is 75% of the square's area?

Answer 1

Its 1.5 units

Explanation:

Answer 2

Length of the rectangle is either 0.5 units or 1.5 units.

Explanation:

Given:

Perimeter of a unit square is equal to the perimeter of a rectangle.

Area of rectangle is 75 % of the square's area.

Unit square means a square of side length 1 unit.

So, perimeter of a unit square,
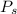`P_(s)`, is sum of all the 4 sides and is equal to:

`P_(s)=4* 1=4`

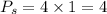
Therefore, perimeter of the rectangle is,
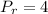`P_(r)=4` units.

Now, perimeter of rectangle of length
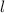`l` and width
`b` is given as:

`P_(r)=2(l+b)`

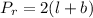
Therefore,

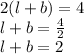`2(l+b)=4\\l+b=(4)/(2)\\l+b= 2` --------1

Again, area of a unit square is 1 square units.

So, area of rectangle 0.75 of 1 which is 0.75 square units.

Or,
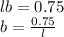`lb=0.75\\b=(0.75)/(l)`--------2

Plug in
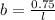`b=(0.75)/(l)` in equation 1, we get

`l+(0.75)/(l)=2\\l^(2)+0.75=2l\\l^(2)-2l+0.75=0\\(l-0.5)(l-1.5)=0\\l=0.5\textrm{ or } l=1.5`

`l=0.5 \textrm{ or }l= 1.5`

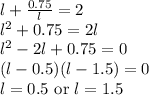
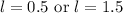
Therefore, the length of the rectangle is 0.5 units or 1.5 units.