Answer:
The given function is
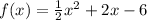
First, we need to find the zeros of the quadratic function, which represent the interception with the x-axis:

So, the graph of this function has two interception points with x-axis, which are
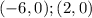
Now, we have to find the vertex of the function to draw it:
The horizontal coordinate of the vertex is

The vertical coordinate of the vertex is
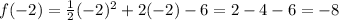
So, the vertex is at
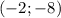
The graph would be as the image attached.