Question

Aloop of wire of area 71 cm^2 is placed with its plane parallel to a 16 mt magnetic field. the loop is then rotated so that its plane is perpendicular to the field, in a time of 0.7 s. what is the average emf generated in the coil while the loop is rotating, in units of volts?

Answer 1

Approximately 1.62 × 10⁻⁴ V.

Step-by-step explanation:

The average EMF in the coil is equal to

`\displaystyle \frac{\text{Final Magnetic Flux} - \text{Initial Magnetic Flux}}{2}`,

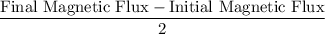Why does this formula work?

By Faraday's Law of Induction, the EMF
`\epsilon` induced in a coil (one loop) is equal to the rate of change in the magnetic flux
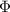`\Phi` through the coil.

`\displaystyle \epsilon(t) = (d)/(dt)(\Phi(t))`.

Finding the average EMF in the coil is similar to finding the average velocity.

`\displaystyle \text{Average}\; \epsilon = (1)/(t)\int_0^t \epsilon(t)\cdot dt`.

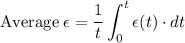However, by the Fundamental Theorem of Calculus, integration reverts the action of differentiation. That is:

`\displaystyle \int_0^(t) \epsilon(t)\cdot dt = \int_0^(t) (d)/(dt)\Phi(t)\cdot dt = \Phi(t) - \Phi(0)`.

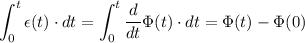Hence the equation

`\displaystyle \text{Average}\; \epsilon = (1)/(t)\int_0^t \epsilon(t)\cdot dt = (\Phi(t)- \Phi(0))/(t)`.

Note that information about the constant term in the original function will be lost. However, since this integral is a definite one, the constant term in
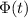`\Phi(t)` won't matter.

Apply this formula to this question. Note that
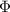`\Phi`, the magnetic flux through the coil, can be calculated with the equation

`\Phi = B \cdot A \cdot N \; sin(\theta)`.

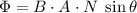For this question,

• 
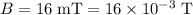  `B = \rm 16\; mT = 16* 10^(-3)\; T` is the strength of the magnetic field.
• 
  `A = \rm 71\; cm^(2) = 71* \left(10^(-2)\right)^2 \; m^(2)` is the area of the coil.
• 
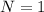  `N = 1` is the number of loops in the coil.
• 
  `\theta` is the angle between the field lines and the coil.
• At
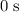  `\rm 0\;s`, the field lines are parallel to the coil,
  `\theta = 0^(\circ)`.
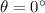• At
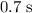  `\rm 0.7\; s`, the field lines are perpendicular to the coil,
  `\displaystyle \theta = 90^(\circ)`.

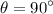Initial flux:
`\Phi(0)= 0`.

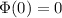Final flux:
`\Phi(0.7) = \rm 1.1136* 10^(-4)\; Wb`.

Average EMF, which is the same as the average rate of change in flux:

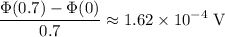`\displaystyle (\Phi(0.7) - \Phi(0))/(0.7) \approx\rm 1.62* 10^(-4)\; V`.