Answer:
Proof is below.
Explanation:
If two sides are equal, then angles opposite to them are also equal.
The angle opposite to the greater side is greater than the angle opposite to lesser side.
Given:
In
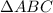 ,
,
AB = AC
PC > PB
As sides AB = AC,
∴
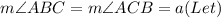
As PC > PB, then, from the theorem of greater angle lies opposite to the greater side,
∴
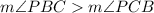
Let
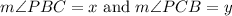
So, angle PBA is,

Angle PCA is,

Now, we have,
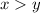
Multiply by -1 both sides. This changes the inequality sign.
⇒
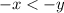
Adding
 on both sides, we get
on both sides, we get
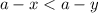
But,
 and
and
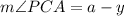 .
.
∴
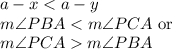 . Hence, it is proved.
. Hence, it is proved.