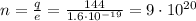A) 144 C
The electric current is defined as
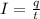
where
q is the charge passing a given point of the circuit in a given time
t is the time interval considered
For this bulb, we know that:
I = 0.20 A is the current
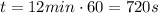 is the time considered
is the time considered
Therefore, the amount of charge passing the point in the circuit in this time is
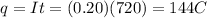
B)
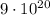 electrons
electrons
The charge of one electron is
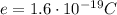
And the total charge passing through the point in the circuit in 12 min is
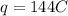
So the total charge can be written as
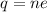
where
n is the number of electrons passing that point of the circuit in 12 min
So, solving for n,