Question

A parabola can be drawn given a focus of

(
2
,
8
)
(2,8) and a directrix of
y
=
10
y=10. Write the equation of the parabola in any form.

Answer 1

`y=-(1)/(4)(x-2)^(2)+9`

Explanation:

Any point on a given parabola is equidistant from focus and directrix.

Given:

Focus of the parabola is at
`(2,8)`.

Directrix of the parabola is
`y=10`.

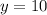Let
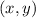`(x,y)` be any point on the parabola. Then, from the definition of a parabola,

Distance of
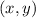`(x,y)` from focus = Distance of
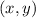`(x,y)` from directrix.

Therefore,

`\sqrt{(x-2)^(2)+(y-8)^(2)}=|y-10|`

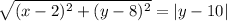
Squaring both sides, we get

`(x-2)^(2)+(y-8)^(2)=(y-10)^(2)\\(x-2)^(2)=(y-10)^(2)-(y-8)^(2)\\(x-2)^(2)=(y-10+y-8)(y-10-(y-8))...............[\because a^(2)-b^(2)=(a+b)(a-b)]\\(x-2)^(2)=(2y-18)(y-10-y+8)\\(x-2)^(2)=2(y-9)(-2)\\(x-2)^(2)=-4(y-9)\\y-9=-(1)/(4)(x-2)^(2)\\y=-(1)/(4)(x-2)^(2)+9`

Hence, the equation of the parabola is
`y=-(1)/(4)(x-2)^(2)+9`.