Answer:
y - 5 =
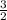 (x - 1)
(x - 1)
Explanation:
Note that
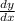 =
=
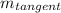
Differentiate using the power rule
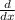 (a
(a
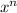 ) = na
) = na
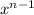
Given
y = x
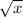 = x.
= x.
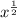 =
=
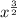 , then
, then
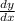 =
=
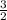
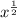
When x = 1
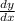 =
=
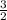 . 1 =
. 1 =
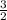
The equation of a line in point- slope form is
y - b = m(x - a)
where m is the slope and (a, b) a point on the line
Here m =
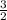 and (a, b) = (1, 5), thus
and (a, b) = (1, 5), thus
y - 5 =
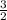 (x - 1) ← equation of tangent
(x - 1) ← equation of tangent