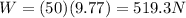Question

The radius of the earth is 6380 km and the height of mt.everest is 8848 m. if the value of of acceleration due to gravity on the top of mt.everest is 9.77m\s , calculate the value of acceleration due to gravity on the surface of the earth . what is the weight of mass 50 on the top of mt.everest ?​

Answer 1

a)
`9.80 m/s^2`

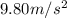
The acceleration due to gravity at a certain location on Earth is given by

`g=(GM)/((R+h)^2)`

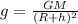
where

G is the gravitational constant

M is the Earth's mass

R is the Earth's radius

h is the altitude above the Earth's surface

At the top of Mt. Everest,

R = 6380 km =
`6.38\cdot 10^6 m`

`h' = 8848 m`

`g'=9.77 m/s^2`

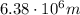
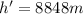
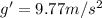
With

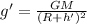`g'=(GM)/((R+h')^2)` (1)

At the Earth's surface,

R = 6380 km =
`6.38\cdot 10^6 m`

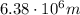
h = 0

g = ?

So

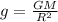`g=(GM)/(R^2)` (2)

By doing the ratio (2)/(1), we find an expression for g in terms of g':

`(g)/(g')=((GM)/(R^2))/((GM)/((R+h')^2))=((R+h')^2)/(R^2)=((6.38\cdot 10^6+8848)^2)/((6.38\cdot 10^6)^2)=1.003`

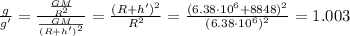
And therefore,

`g=1.009g'=1.009(9.77)=9.80 m/s^2`

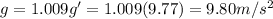
b) 519.3 N

The weight of an object near the Earth's surface is given by

`W=mg`

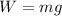
where

m is the mass of the object

g is the acceleration of gravity at the object's location

In this problem,

m = 50 kg is the mass of the object

g' = 9.77 m/s^2 is the acceleration of gravity on top of Mt Everest

Susbtituting,

`W=(50)(9.77)=519.3 N`