Answer: 40 L of 80 percent solution and 60 L of 30 percent solution
Explanation:
The total mixture of 100 L of apple juice of
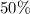 solution must contain:
solution must contain:
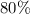 solution of apple juice ---> Let's call it
solution of apple juice ---> Let's call it

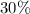 solution of apple juice ---> Let's call it
solution of apple juice ---> Let's call it

So, we can set these values in a table taking into account
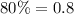 ,
,
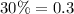 and
and
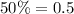 :
:
![\left[\begin{array}{ccccc}&apple-juice (L)&Percent&Total\\80\% Juice&x&0.8&0.8 x\\30\% juice&y&0.3&0.3 y\\Mixture&x+y=100&0.5&0.5(100)\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/o21ygv1quio27o9oji39p7orsff2hlrqho.png)
Now, with the information of the
 column we can write the first equation:
column we can write the first equation:
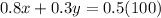 (1)
(1)
And with the information of the
 column, the second equation:
column, the second equation:
 (2)
(2)
At this point we are able to calculate how many litters have
 and
and
 .
.
Isolating
 from (2):
from (2):
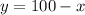 (3)
(3)
Substituting (3) in (1):
 (4)
(4)
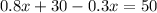
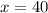 (5) 40 L of solution A
(5) 40 L of solution A
Substituting (5) in (2):
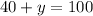 (6)
(6)
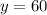 (7) 60 L of solution B
(7) 60 L of solution B
Therefore, the cafeteria worker needs to mix 40 L of solution A with 60 L of solution B.