Answer:
The Height of the tower is 188.67 ft
Explanation:
Given as :
The angle of elevation to tower = 15°
The distance travel closer to tower the elevation changes to 42° = 497 ft
Now, Let the of height of tower = h ft
The distance between 42° and foot of tower = x ft
So, The distance between 15° and foot of tower = ( x + 497 ) ft
So, From figure :
In Δ ABC
Tan 42° =

Or , Tan 42° =
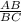
Or, 0.900 =
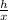
∴ h = 0.900 x
Again :
In Δ ABD
Tan 15° =

Or , Tan 15° =

Or, 0.267 =

Or, h = ( x + 497 ) × 0.267
So, from above two eq :
0.900 x = ( x + 497 ) × 0.267
Or, 0.900 x - 0.267 x = 497 × 0.267
So, 0.633 x = 132.699
∴ x =
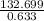
Or, x = 209.63 ft
So, The height of tower = h = 0.900 × 209.63
Or, h = 188.67 ft
Hence The Height of the tower is 188.67 ft Answer