Question

Find the value of c so that (x + 1) is a factor of the polynomial p(x).

p(x) = 5x^4 + 7x^3– 2x^2– 3x + c
C=
Find c for me pleasese

Answer 1

1

Explanation:

Answer 2

The value of c so that (x + 1) is a factor of the polynomial p(x) = 5x^4 + 7x^3– 2x^2– 3x + c is equal to 1

Solution:

Given polynomial is as follows

`\mathrm{p}(x)=5 x^(4)+7 x^(3)-2 x^(2)-3 x+\mathrm{c}`

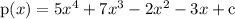
Also given that (x+1) is factor of given polynomial p(x).

Need to determine value of constant c.

We will be solving above problem using factor theorem.

Factor theorem says that if ( x – a) is a factor of any polynomial f(x) , then f(a) = 0.

As in our case f(x) = p(x) and factor of p(x) is (x + 1) , which can be rewritten as (x – ( -1)) , so "a" in our case is -1 .

According to factor theorem p(-1) = 0

On substituting x = -1 , in given expression of p(x) we get

`\begin{array}{l}{\mathrm{p}(-1)=5(-1)^(4)+7(-1)^(3)-2(-1)^(2)-3(-1)+\mathrm{c}} \\\\ {\mathrm{p}(-1)=5-7-2+3+\mathrm{c}} \\\\ {\mathrm{p}(-1)=\mathrm{c}-1} \\\\ {\text { As } \mathrm{p}(-1)=0, \mathrm{c}-1=0} \\\\ {=>\mathrm{c}=1}\end{array}`

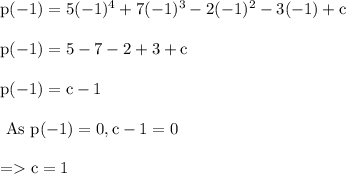
Hence value of c in the given polynomial is 1