Question

The length of the hypotenuse of a right angled triangle exceeds the length of the base by 2cm and exceeds twice the length of the altitude by 1cm.Find the length of each side of the triangle​

Answer 1

Answer: a = 8; b = 15; c = 17

Explanation:

c = b + 2 and c = 2a + 1

b = c − 2 and a =
`(c-1)/(2)`

​

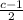
c² = b² + a²

`c^(2) = (c-2)^(2) + (c-1)/(2)\\`

`c^(2)= (4 (c-2)^(2)+(c - 1)^(2) )/(4)`

`4c^(2)={4 (c^(2) + 4 -4c)+c ^(2) + 1-2c`

`4c^(2)={4 c^(2) + 16 -16c)+c ^(2) + 1-2c`

`c^(2)-18c+17=0`

`c(c -17)-1(c-17)=0`

​
`(c -1)(c-17)=0`

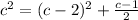
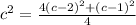
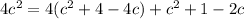
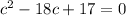
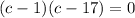
c = 1 or c = 17

If c = 1 then b = 1 - 2 = -1, that's not possible

So x = 17

b = 17 - 2 = 15

a =
`(17-1)/(2) = 8`

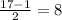
Length sides of the triangle are 17 cm, 15 cm and 8 cm.

I saw some of this on a site but I want to make sure its correct so we're gonna apply the pythagorean theory and see if its correct.

`a^(2) + b^(2) = c^(2) \\8^(2) + 15^(2) = 17^(2) \\64 + 225 = 289\\289 = 289\\`

This shows that this is correct.

Hope this helped! Again, some of this was from a site, not from me.