Answer:
a) 64 feet
b) 3 seconds
Explanation:
a)
The maximum height of
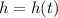 can be bound by finding the y-coordinate of the vertex of
can be bound by finding the y-coordinate of the vertex of
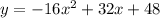 .
.
Compare this equation to
 to find the values of
to find the values of
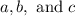 .
.

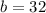
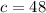 .
.
The x-coordinate of the vertex can be found by evaluating:
![(-b)/(2a)=\frac{-32}{2(-16)]()
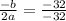
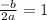
So the x-coordinate of the vertex is 1.
The y-coordinate can be found be evaluating
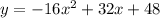 at
at
 :
:
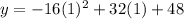
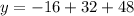

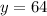
So the maximum height of the rocket is 64 ft high.
b)
When the rocket hit's the ground the height that the rocket will be from the ground is 0 ft.
So we are trying to find the second t such that:
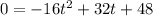
I'm going to divide both sides by -16:
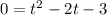
Now we need to find two numbers that multiply to be -3 and add to be -2.
Those numbers are -3 and 1 since (-3)(1)=-3 and (-3)+(1)=-2.
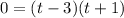
This implies we have either
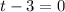 or
or

The first equation can be solved by adding 3 on both sides:
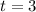 .
.
The second equation can be solved by subtracting 1 on both sides:
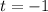 .
.
So when
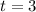 seconds, is when the rocket has hit the ground.
seconds, is when the rocket has hit the ground.