Question

Which type of triangle is formed by joining the vertices A(-3, 6), B(2, 1), and C(9, 5)?

A.
an equilateral triangle
B.
an acute scalene triangle
C.
a right triangle
D.
an obtuse scalene triangle

Answer 1

An obtuse scalene triangle

Explanation:

First, we calculate the length of the sides:

Side a – the distance between points B and C – is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)\\d=√((9-2)^2+(5-1)^2)\\d=√((7)^2+(4)^2)\\d=√(49+16)\\d=√(65)\\d\approx{8.06}`

Side b – the distance between points C and A – is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)\\d=√((-3-9)^2+(6-5)^2)\\d=√((-12)^2+(1)^2)\\d=√(144+1)\\d=√(145)\\d\approx{12.04}`

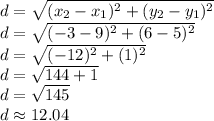
Side c – the distance between points A and B – is:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)\\d=√((2-(-3))^2+(1-6)^2)\\d=√((5)^2+(-5)^2)\\d=√(25+25)\\d=√(50)\\d\approx{7.07}`

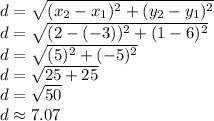
Then, we calculate the measure of the angles:

`\angle{A}=\textrm{arccos}((b^2+c^2-a^2)/(2bc))=\textrm{arccos}((12.04^2+7.07^2-8.06^2)/(2(12.04)(7.07)))\approx{40.23^(\circ)}`

`\angle{B}=\textrm{arccos}((a^2+c^2-b^2)/(2ac))=\textrm{arccos}((8.06^2+7.07^2-12.04^2)/(2(8.06)(7.07)))\approx{105.27^(\circ)}`

`\angle{C}=180^(\circ)-40.23^(\circ)-105.27^(\circ)=34.50^(\circ)`

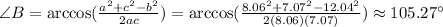
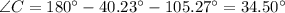
None of the sides are equal, so the triangle is not equilateral nor isosceles. None of the angles are 90°, so the triangle is not right. One of the angles is greater than 90°, so the triangle must be obtuse scalene.