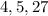Answer:
4,5,27
Problem:
Boris chose three different numbers.
The sum of the three numbers is 36.
One of the numbers is a perfect cube.
The other two numbers are factors of 20.
Explanation:
Let's pretend those numbers are:
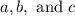 .
.
We are given the sum is 36:
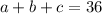 .
.
One of our numbers is a perfect cube.
 where
where
 is an integer.
is an integer.
The other two numbers are factors of 20.
 and
and
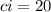 where
where
 .
.
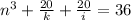
From here I would just try to find numbers that satisfy the conditions using trial and error.
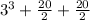
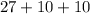


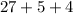

So I have found a triple that works:

The numbers in ascending order is: