Question

Find the equation of the line that passes through (−3, 2) and the intersection of the lines x+2y=0 and 3x+y+5=0.

Answer 1

Hence the Equation of line with points ( - 3 , 2) and slop - 1 is Y + X + 1 = 0 Answer

Explanation:

Given two line equation as

x + 2y = 0 And

3x + y + 5 = 0

Now, intersection point of this two lines is :

Solve the given two line equations

Multiply eq 1 by 3,

So ,

3x + 6y = 0

3x + y = - 5

Again , (3x + 6y) - (3x + y) = 5

Or, 5y = 5

I.e y = 1

Put the value of y in above eq

So, 3x + ( 1) = - 5

Or, 3x + 1 = -5

I.e 3x = - 6

So, x = -2

Now equation of line with points ( - 3, 2 ) and ( -2 , 1) is

First we find the slop ( m ) =
`((y2 - y1))/((x2 - x1))`

m =
`((1 - 2))/((- 2 + 3))`

Or, m = - 1

Or, m = -1

∴ Equation of line with points ( - 3 , 2) and slop -1 is

Y - y1 = m (X - x1)

Y - 2 = -1 (X + 3)

Or, Equation of line is Y + X + 1 = 0

Hence the Equation of line with points ( - 3 , 2) and slop - 1 is Y + X + 1 = 0 Answer

Answer 2

The equation of the line is y + x + 1 = 0.

Explanation:

The given equations are : x + 2y = 0 and 3x + y + 5 = 0

Now, finding the intersection point of the above system:

from (1) , x = -2y

put in (2), 3 (-2y) + y + 5 = 0

or, 5y = 5 ,or y = 1

If y = 1, pitting in (1), x = -2

So, the intersection lines is (-2,1).

the other point on line is (-3,2)

Now, finding the slope m of the line :
`m =(y_2 -y_1)/(x_2 - x_1)  =(2 -1)/(-3 - (- 2))`

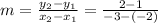
or,
`m = -(1)/(1)` = -1

So, by POINT SLOPE FORM: the equation of a line is

(y - y0) =m (x -x0),

now for (-3,2) : equation is ( y - 2) = (-1) (x +3)

or, y + x + 1 = 0

Hence, the equation of the line that passes through (−3, 2) and the intersection of the lines x+2y=0 and 3x+y+5=0 is y + x + 1 = 0.