Question

Based on the shortest leg of the triangle illustrated, if a similar triangle on the coordinate plane has its shortest leg defined by the points (1, 9) and (4, 8), what is the third point?

A) (1, 2)
B) (1, 1)
C) (2, 1)
D) (2, 2)

Answer 1

C. (2,1)

Explanation:

Shortest leg in triangle ABC is leg AB, shortest leg in triangle A'B'C' is leg A'B'.

Find distances AB and A'B':

`AB=√((-2-(-8))^2+(8-10)^2)=√(36+4)=√(40)=2√(10)\\ \\A'B'=√((4-1)^2+(8-9)^2)=√(9+1)=√(10)`

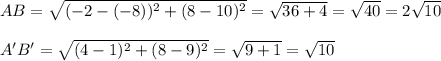
So, the coefficient of similarity is
`(1)/(2)` (triangle A'B'C' is
`(1)/(2)` of triangle ABC).

If we go from point B to point C 14 units down and 4 units left, then we go from point B' to point C' 7 units down and 2 units left.

If point B' has coordinates (4,8), then point C' has coordinates (4-2,8-7) that is (2,1).