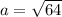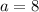Question

Find the length of an equilateral triangle having an area of 16
`√(3)`
`cm^(2)`

Answer 1

8 cm

Explanation:

An equilateral triangle has 3 sides all being congruent to each other.

If I draw a line segment from one vertex to the opposite side at it's midpoint, I would have halved the triangle into two right triangles.

Let's each side of this equilateral triangle have measurement,
`a`.

Let
`h` be the height of the triangle:

`((a)/(2))^2+h^2=a^2`

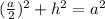
Let's solve for h in terms of
`a`.

`(a^2)/(4)+h^2=a^2`

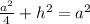
Subtract
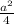`(a^2)/(4)` on both sides:

`h^2=a^2-(a^2)/(4)`

`h^2=(4)/(4)a^2-(1)/(4)a^2`

`h^2=(4-1)/(4)a^2`

`h^2=(3)/(4)a^2`

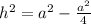
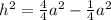
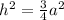
Now square root both sides:

`h=(√(3))/(2)a`

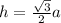
So the area of the triangle is
`(1)/(2) \cdot a \cdot (√(3))/(2)a`.

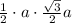Let's simplify that a bit:
`(√(3))/(4)a^2`.

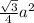We are also given a numerical value for the area,
`16√(3)`.

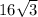So this will give us the equation
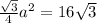`(√(3))/(4)a^2=16√(3)` so that we can solve for
`a`.

Multiply both sides by
`(4)/(√(3))`:

`a^2=16 √(3) \cdot (4)/(√(3))`

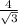Simplify the right hand side:

`a^2=16 \cdot 4`

`a^2=64`

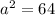
Take the square root of both sides:

`a=√(64)`

`a=8`

Answer 2

Thus , The length of each side of the given equilateral triangle is 8