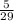Question

In a certain Algebra 2 class of 29 students, 7 of them play basketball and 24 of them play baseball. There are 3 students who play neither sport. What is the probability that a student chosen randomly from the class plays both basketball and baseball?

Answer 1

`(5)/(29)`

Explanation:

Let
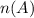`n(A)` represent students playing basketball,
`n(B)` represent students playing baseball.

Then,
`n(A)=7`,
`n(B)=24`

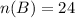
Let
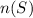`n(S)` be the total number of students. So,
`n(S)=29`.

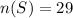Now,

`P(A)=(n(A))/(n(S))=(7)/(29)`

`P(B)=(n(B))/(n(S))=(24)/(29)`

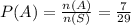
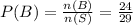
3 students play neither of the sport. So, students playing either of the two sports is given as:

`n(A\cup B)=n(S)-3\\n(A\cup B)=29-3=26`

∴
`P(A\cup B)=(n(A\cup B))/(n(S))=(26)/(29)`

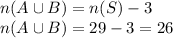
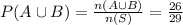
From the probability addition theorem,

`P(A\cup B)=P(A)+P(B)-P(A\cap B)`

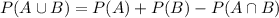
Where,
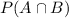`P(A\cap B)` is the probability that a student chosen randomly from the class plays both basketball and baseball.

Plug in all the values and solve for
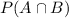`P(A\cap B)` . This gives,

`(26)/(29)=(7)/(29)+(24)/(29)+P(A\cap B)\\\\(26)/(29)=(7+24)/(29)+P(A\cap B)\\\\(26)/(29)=(31)/(29)+P(A\cap B)\\\\P(A\cap B=(31)/(29)-(26)/(29)\\\\P(A\cap B=(31-26)/(29)=(5)/(29)`

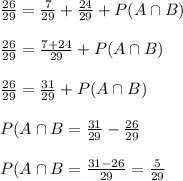
Therefore, the probability that a student chosen randomly from the class plays both basketball and baseball is
`(5)/(29)`