Answer:
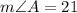 °
°
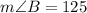 °
°
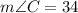 °
°
Explanation:
Let the measure of angle C be
 °.
°.
Given:
In triangle ΔABC,
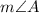 is thirteen less than
is thirteen less than
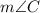 and
and
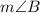 is eleven less than four times
is eleven less than four times
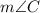 . This gives,
. This gives,
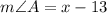
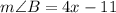
Also,
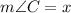
Now, for a triangle, the sum of all its interior angles is equal to 180°.
Therefore,
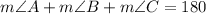
Plug in all the values and solve for x. This gives,
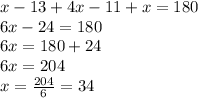
Therefore, measure of angle C is 34°.
Measure of angle A is,
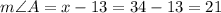 °.
°.
Measure of angle B is,
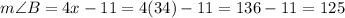 °.
°.