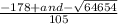Question

7 (r3+15r² +48r – 44) = (r+6)​

Answer 1

`(-178 + and - √(64654) )/(105)`

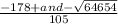
Explanation:

Advanced equations like these fit perfect to do the quadratic formula

first we must find a,b and c

A=
`x^(2)`

B=constant multiplied by x

C=constant not multiplied by x

Alright now that we established that we need to format the equation to equal 0 so it will basically look like this
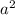`a^(2)`+b+c=0

First add like terms

7 (51r +
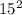`15^(2)` -44) = r + 6

Then we do the distributive property

357r +
`105r^(2)` -308 = r + 6

Then we inverse the R + 6 so we can make the equation equal 0

so 357r +
`105r^(2)` -308-r-6 = 0

Add like terms again

356r +
`105r^(2)` -314=0

Now we have our A B and C!!! So lets put it in the quadratic formula

I like to find the discriminant first which is
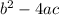`b^(2) -4ac` so lets plug everything in.

356
`356^(2) -4(105)(-314)`

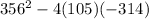
and that equals

258616 but that isn't a perfect square so we'll need to factor it so lets keep it fragmented for the time being

`\frac{-316+ and -\sqrt{356^(2)+131880 } }{210}`

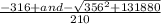
is our current expression

The easiest thing to factor out is
`2^(2)`

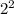
So that should equal

`\frac{-356+ and -\sqrt{2^(2) *64654} }{210}`

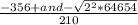
Square
`2^(2)`

`(-356+and-2√(64654) )/(210)`

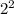
now the only thing left to do is divided every thing by the greatest common factor which is 2, we don't divided whatever is in the
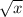`√(x)` when doing this step

so the final solution is

`(-178+ and -√(64654) )/(105)`

Answer 2

r=−9.403283,−6.348173,0.751456

Explanation:

Let's solve your equation step-by-step.

7(r3+15r2+48r−44)=r+6

7r3+105r2+336r−308=r+6

Step 1: Subtract r+6 from both sides.

7r3+105r2+336r−308−(r+6)=r+6−(r+6)

7r3+105r2+335r−314=0

Step 2: Use cubic formula.

r=−9.403283,−6.348173,0.751456