The
 th number in the sequence can be expressed as
th number in the sequence can be expressed as
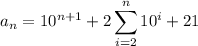
Extracting the
 th term from the sum gives
th term from the sum gives

and
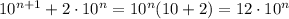 . 3 divides both 12 and 21, so
. 3 divides both 12 and 21, so
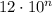 and 21 contribute no remainder.
and 21 contribute no remainder.
This leaves us with
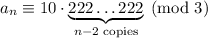
Recall that a decimal integer is divisible by 3 if its digits add to a multiple of 3. The digits in
 are
are
 copies of 2 and one 0, so the digital sum is
copies of 2 and one 0, so the digital sum is
 .
.
- If
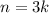 for
for
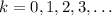 , then the digital sum is
, then the digital sum is
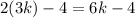 , which is not divisible by 3.
, which is not divisible by 3. - If
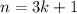 , then the sum is
, then the sum is
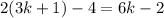 , which is not divisible by 3.
, which is not divisible by 3. - If
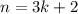 , then the sum is
, then the sum is
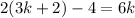 , which is always divisble by 3.
, which is always divisble by 3.
This means that roughly 1/3 of the first
 numbers in this sequence are divisible by 3; among the first 100 terms, they occur for
numbers in this sequence are divisible by 3; among the first 100 terms, they occur for
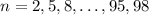 , of which there are 33.
, of which there are 33.