Question

The path of his motorcycle was given approximately by H=-0.005x^2+2.39x+600 where H was measured in ft above the river and x was the distance from his launch ramp. How high above the river was the launch ramp? I found that the maximum height was 600ft and the horizontal distance was 234ft.​

Answer 1

H = 600 ft.

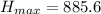`H_(max) =885.6` ft at x =239 ft.

Explanation:

The path of a motorcycle is given by
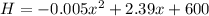`H =-0.005x^(2)+2.39x + 600` .....(1) where H is the height above the river in ft and x is the distance from his launch camp.

Putting x = 0, the height of the launch camp from the river is H = 600 ft.

Now. differentiating equation (1), with respect to x both sides we get,

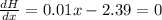`(dH)/(dx) = 0.01x -2.39 =0` {Condition for H to be maximum is
`(dH)/(dx) =0`}

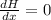⇒ x = 239 ft.

So,
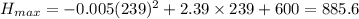`H_(max) = -0.005 (239)^(2) + 2.39 * 239 + 600 =885.6` ft. (Answer)