Answer:
From given relation the value of β is 37.5°
Explanation:
Given as :
α and β are two acute angles of right triangle
Acute angle have measure less than 90°
Now given as :
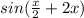 =
=
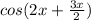
Or,
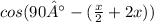 =
=
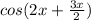
SO,
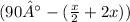 =
=
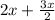
Or, 90° =
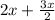 +
+

or, 90° =
 + 4x
+ 4x
Or, 90° =
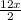
So, x =
 = 15°
= 15°
∴
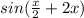 =
=
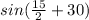
So,
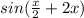 = sin
= sin
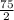
∴ The value of Ф_1 =
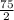 = 37.5°
= 37.5°
Similarly
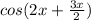 =
=
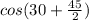
So ,The value of Ф_2 =
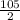 = 52.5°
= 52.5°
∵ β
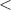 α
α
So, As 37.5°
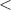 52.5°
52.5°
∴ β = 37.5°
Hence From given relation the value of β is 37.5° Answer