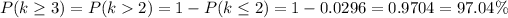Question

Customers arrivals at a checkout counter in a department store per hour have a Poisson distribution with parameter λ = 7. Calculate the probabilities for the following events.(1) (2 points) Exactly seven customers arrive in a random 1-hour period.(2) (4 points) No more than two customers arrive in a random 1-hour period.(3) (4 points) At least three customers arrive in a random 1-hour period

Answer 1

(1)14.9% (2) 2.96% (3) 97.04%

Explanation:

Formula for Poisson distribution:
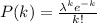`P(k) = (\lambda^ke^(-k))/(k!)` where k is a number of guests coming in at a particular hour period.

(1) We can substitute k = 7 and
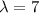`\lambda = 7` into the formula:

`P(k=7) = (7^7e^(-7))/(7!)`

`P(k=7) = (823543*0.000911882)/(5040) = 0.149 = 14.9\%`

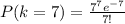
(2)To calculate the probability of maximum 2 customers, we can add up the probability of 0, 1, and 2 customers coming in at a random hours

`P(k\leq2) = P(k=0)+P(k=1)+P(k=2)`

`P(k\leq2) = (7^0e^(-7))/(0!) + (7^1e^(-7))/(1!) + (7^2e^(-7))/(2!)`

`P(k \leq 2) = (0.000911882)/(1) + (7*0.000911882)/(1) + (49*0.000911882)/(2)`

`P(k\leq2) = 0.000911882+0.006383174+0.022341108 \approx 0.0296=2.96\%`

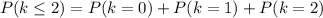
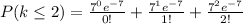
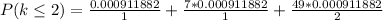
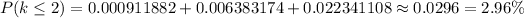
(3) The probability of having at least 3 customers arriving at a random hour would be the probability of having more than 2 customers, which is the invert of probability of having no more than 2 customers. Therefore:

`P(k\geq 3) = P(k>2) = 1 - P(k\leq2) = 1 - 0.0296 = 0.9704 = 97.04\%`