Answer:
If n=1, l can only have the value l=0 and the total number of orbitals is 0. If l=1, ml can be -1,0 or 1 and the total number of orbitals at l=1 is 3.
Step-by-step explanation:
When solving the radial part of Schrödinger equation, one needs to expand in power series that lead to Laguerre polynomials of the form
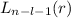, being n and l the quantum numbers. As is known, in the Laguerre polynomials the subindex must be greater than or equal to 0, which implies
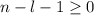. So if n=1, the only possible value of l is l=0.
Likewise, when solving the angular part, one gets the spherical harmonics
![Y_(l,m_l)(\theta,\phi)[\tex] as solution. One of the properties of spherical harmonics is that the number [tex]m_l[\tex] can only take the values [tex]m_l=-l,-l+1,-l+2,...,l-1,l[\tex]. So if l=0, as above, [tex]m_l[\tex] can only take the value [tex]m_l=0,[\tex] thus giving only 1 orbital. But if l=1, [tex]m_l]()
can be
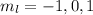. Therefore the sublevel l=| has 3 possible orbitals.