Question

Let L be the line parametrized by x = 2 + 2t, y = 3t, z = −1 − t. (a) Find a linear equation for the plane that is perpendicular to L and includes the point (2, 0, −1). (b) Where does L intersect the plane x + 2y + 3z = 9?

Answer 1

Explanation:

Given that L is a line parametrized by

`x = 2 + 2t, y = 3t, z = −1 − t`

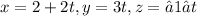
The plane perpendicular to the line will have normal as this line and hence direction ratios of normal would be coefficient of t in x,y,z

i.e. (2,3,-1)

So equation of the plane would be of the form

`2x+3y-z =K`

Use the fact that the plane passes through (2,0,-1) and hence this point will satisfy this equation.

`2(2)+3(0)-(-1) =K\\K =5`

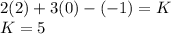
So equation is

`2x+3y-z =5`

b) Substitute general point of L in the plane to find the intersecting point

`2(2+2t)+3t-(-1-t) =5\\4+8t+1=5\\8t=0\\t=0\\(x,y,z) = (2,0,-1)`

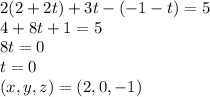
i.e. same point given.