Question

PLEASEE can someone help me with this and show the work

Answer 1

Width to give maximum area is 12 feet. Maximum area is 144 square feet.

Explanation:

Given:

Width is given as
`x`.

Area of the rectangular pen is given as,
`A=24x-x^(2)`

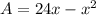
For maximum area, the derivative of area with respect to
`x` must be 0. So,

`\frac{dA}{\mathrm{d} x}=\frac{\mathrm{d} }{\mathrm{d} x}(24x-x^(2))\\0=24-2x\\2x=24\\x=(24)/(2)=12`

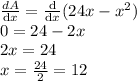
Therefore, for maximum area, the width should be 12 feet.

Now, plug in 12 ft for
`x` in the expression for area to calculate maximum area. This gives,

Maximum area,
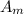`A_(m)`, is given as:

`A_(m)=24x-x^(2)\\A_(m)=24(12)-12^(2)=288-144=144\textrm{ }ft^(2)`

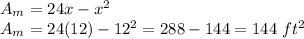
Therefore, the maximum area is 144 square feet.