Answer:
a)
 ≈0.33
≈0.33
b)
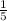 = 0.2
= 0.2
c) 1
Explanation:
This is a conditional probability problem.
Let P(F)= the probability that the gambler selects fair coin
P(TH) = the probability that the gambler selects two head coin
P(H|TH)= the probability of getting heads given that the gambler selects two headed coin.
P(H|F)= probability of getting heads given that the gambler selects fair coin
P(F|H)= probability of the gambler selects fair coin given that it shows head after flipping
P(H)= the probability of getting heads
P(HH)=the probability of getting two heads
Since gambler selects coins randomly P(F)=P(TH)= 0.5, P(H|F)=0.5 since the coin is fair.
We have also this conditional probability equation:
P(F|H) =
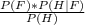
a) For the first case P(H)= P(H|F)×P(F)+P(H|TH)×P(TH)=
 ×
×
 +1×
+1×
 =
=
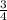 =0.75
=0.75
If we put the numbers in conditional probability formula:
P(F|H) =
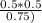 =
=
 ≈0.33
≈0.33
b) For flipping twice:
P(HH)= P(HH|F)×P(F)+P(HH|TH)×P(TH) =
 ×
×
 +1×
+1×
 =
=
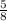 =0.625
=0.625
then our formula becomes:
P(F|HH) =
 =
=
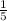 =0.2
=0.2
c) For flipping third time:
When flipping for the third time and it shows tails, then the coin cannot be two heads coin since it has 0 probability of getting tails. Therefore for this case the P(F|T)= the probability of choosing fair coin given that it shows tails)=1