Answer:
![[T]EE=\left[\begin{array}{ccc}2&3&3\\6&4&4\\-2&3&4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/o5z68lkypsg1vjc73mfjak5hpkocj27j2a.png)
Explanation:
First we start by finding the dimension of the matrix [T]EE
The dimension is : Dim (W) x Dim (V) = 3 x 3
Because the dimension of P2 is the number of vectors in any basis of P2 and that number is 3
Then, we are looking for a 3 x 3 matrix.
To find [T]EE we must transform the vectors of the basis E and then that result express it in terms of basis E using coordinates and putting them into columns. The order in which we transform the vectors of basis E is very important.
The first vector of basis E is e1(t) = 1
We calculate T[e1(t)] = T(1)
In the equation : 1 = a0
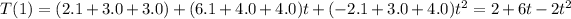
![[T(e1)]E=\left[\begin{array}{c}2&6&-2\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/b9kdqg9ojjo7djpk15xx2oughox3aspvj7.png)
And that is the first column of [T]EE
The second vector of basis E is e2(t) = t
We calculate T[e2(t)] = T(t)
in the equation : 1 = a1
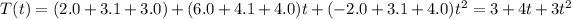
![[T(e2)]E=\left[\begin{array}{c}3&4&3\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/84educ9mg47j7m0ir9k0yalcn25180chtb.png)
Finally, the third vector of basis E is
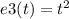
![T[e3(t)]=T(t^(2))](https://img.qammunity.org/2020/formulas/mathematics/college/6ww9sc7522mikp9iwn6e2wcq78b4x9dbpy.png)
in the equation : a2 = 1
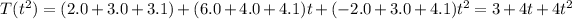
Then
![[T(t^(2))]E=\left[\begin{array}{c}3&4&4\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/zma71fojetfbjuugqiz9gyr4jvrv9morsq.png)
And that is the third column of [T]EE
Let's write our matrix
![[T]EE=\left[\begin{array}{ccc}2&3&3\\6&4&4\\-2&3&4\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/o5z68lkypsg1vjc73mfjak5hpkocj27j2a.png)
T(X) = AX
Where T(X) is to apply the transformation T to a vector of P2,A is the matrix [T]EE and X is the vector of coordinates in basis E of a vector from P2
For example, if X is the vector of coordinates from e1(t) = 1
![X=\left[\begin{array}{c}1&0&0\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/p9gfhj2wa68z68xx0pnmd1pnmqi6i11y6f.png)
![AX=\left[\begin{array}{ccc}2&3&3\\6&4&4\\-2&3&4\end{array}\right]\left[\begin{array}{c}1&0&0\\\end{array}\right]=\left[\begin{array}{c}2&6&-2\\\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/u9zj87fwjk3e5xpvtk24s71rrfzsei646a.png)
Applying the coordinates 2,6 and -2 to the basis E we obtain
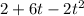
That was the original result of T[e1(t)]