Question

A circular conducting loop with a radius of 0.50 m and a small gap filled with a 10.0-Ω resistor is oriented in the xy-plane. If a uniform magnetic field of 1.0 T, making an angle of 30∘ with the z-axis, increases to 10.0 T, in 4.0 s, what is the magnitude of the current that will be caused to flow in the loop if it has negligible resistance?

Answer 1

Current, I = 0.153 A

Step-by-step explanation:

Given that,

Radius of the circular conducting loop, r = 0.5 m

Resistance of the resistor,
`R=10\ \Omega`

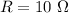
Magnetic field, B = 1 T

Angle with z axis,
`\theta=30^(\circ)`

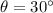
Magnetic field increases to 10 T in 4 seconds

To find,

Magnitude of current.

Solve,

According to Faraday's law, the induced emf is given by:

`\epsilon=(\phi_f-\phi_i)/(t)`

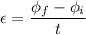
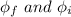`\phi_f\ and\ \phi_i` are final flux and the initial flux respectively.

`\epsilon=NA\ cos\theta(B_f-B_i)/(t)`

`\epsilon=1* \pi (0.5)^2\ cos(30)(10-1)/(4)`

`\epsilon=1.53\ V`

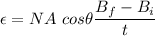
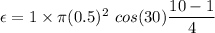
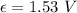
The magnitude of current can be calculated using the Ohm's law as :

`I=(\epsilon)/(R)`

`I=(1.53)/(10)`

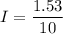
I = 0.153 A

Therefore, the magnitude of the current that will be caused to flow in the loop is 0.153 A.