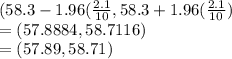Question

A CI is desired for the true average stray-load loss μ (watts) for a certain type of induction motor when the line current is held at 10 amps for a speed of 1500 rpm. Assume that stray-load loss is normally distributed with σ = 2.1. (Round your answers to two decimal places.)

(a) Compute a 95% CI for μ when N = 25 and sample mean = 58.3.
(b) Compute a 95% CI for μ when N = 100 and sample mean = 58.3.

Answer 1

Explanation:

Given that X stray load loss is normal with population std dev = 2.1

Since population std deviation is known we can use Z critical values for finding out confidence intervals

For 95% confidence interval we have formula as

Confidence interval 95% =
`(\bar x-1.96((\sigma)/(√(n) ) ),\bar x+1.96((\sigma)/(√(n) ) )`

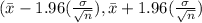
a) Substitute here for x bar = 58.3 and sigma = 2.1,n=25

Confidence interval =
`(58.3-1.96((2.1)/(5),58.3+1.96((2.1)/(5)) \\=(57.4768,59.1232)\\=(57.48, 59.12)`

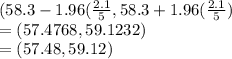
b) NOw we substitute sample size n =100, for same mean and std dev.

Confidence interval =
`(58.3-1.96((2.1)/(10),58.3+1.96((2.1)/(10)) \\=(57.8884,58.7116)\\=(57.89, 58.71)`