Answer:
Explanation:
Let X represent for males and Y for females
Given that
Group Group One Group Two
Mean 84.00 78.00
SD 4.00 8.00
SEM 1.26 2.53
N 10 10
SEM is calculated as
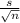 for each group
for each group
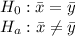
(Two tailed test at 5% significance level)
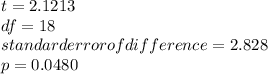
Since p <0.05 we reject H0 and there is significant difference between the groups.
A.Exam scores were significantly higher in the male group, t(18) = 2.83, p < .05B