According to the data presented, the most convenient is to make an approximation through Z-Stadistic Proportions) For the sample size)
So things,
A)
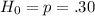
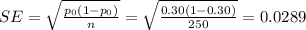
b) Given
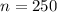 and
and
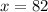 so
so
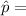 sample proportion
sample proportion
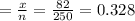
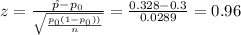
c)
So, A z-value less than 2 or more than 2 is considered unusually small and unusually large respectively,
Then, Since z=0.96<2, the z-test stadistic is unusually small.