Question

A firecracker breaks up into two pieces, one of which has a mass of 200 g and flies off along the x-axis with a speed of 82.0 m/s. The second piece has a mass of 300 g and flies off along the y-axis with a speed of 45.0 m/s. What is the total momentum of the two pieces?

Answer 1

Total momentum, p = 21.24 kg-m/s

Step-by-step explanation:

Given that,

Mass of first piece,
`m_1=200\ g= 0.2\ kg`

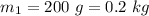
Mass of the second piece,
`m_2=300\ g= 0.3\ kg`

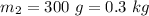
Speed of the first piece,
`v_1=82\ m/s` (along x axis)

Speed of the second piece,
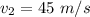`v_2=45\ m/s` (along y axis)

To find,

The total momentum of the two pieces.

Solve,

The total momentum of two pieces is equal to the sum of momentum along x axis and along y axis.

`p_x=m_1v_1`

`p_x=0.2\ kg* 82\ m/s`

`p_x=16.4\ kg-m/s`

`p_y=m_2v_2`

`p_y=0.3\ kg* 45\ m/s`

`p_y=13.5\ kg-m/s`

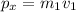
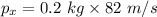
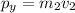
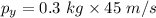
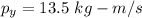
The net momentum is given by :

`p=√(p_x^2+p_y^2)`

`p=√(16.4^2+13.5^2)`

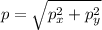
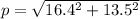
p = 21.24 kg-m/s

Therefore, the total momentum of the two pieces is 21.24 kg-m/s.