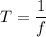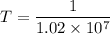Question

An electron of kinetic energy 1.67 keV circles in a plane perpendicular to a uniform magnetic field. The orbit radius is 37.4 cm. Find (a) the electron's speed, (b) the magnetic field magnitude, (c) the circling frequency, and (d) the period of the motion.

Answer 1

Step-by-step explanation:

Given that,

The kinetic energy of the electron,
`K=1.67\ keV=1.67* 10^3\ eV`

Radius of the orbit, r = 37.4 cm = 0.374 m

To find,

(a) the electron's speed, (b) the magnetic field magnitude, (c) the circling frequency, and (d) the period of the motion.

Solve,

We know that,
`1\ eV=1.6* 10^(-19)\ J`

`K=1.67* 10^3* 1.6* 10^(-19)\ J=2.67* 10^(-16)\ J`

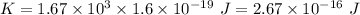
(a) The formula of the kinetic energy is given by :

`K=(1)/(2)mv^2`

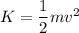
v is the speed if electron

m is the mass of electron

`v=\sqrt{(2K)/(m)}`

`v=\sqrt{(2* 2.67* 10^(-16))/(9.1* 10^(-31))}`

`v=2.42* 10^7\ m/s`

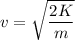
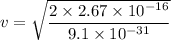
(b) Let B is the magnitude of magnetic field. On the circular path the magnetic field is given by :

`B=(mv)/(qr)`

`B=(9.1* 10^(-31)* 2.42* 10^7)/(1.6* 10^(-19)* 0.374)`

`B=3.68* 10^(-4)\ T`

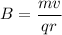
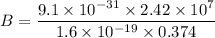
(c) Let T is the time period of the motion. It is given by :

`T=(2\pi r)/(v)`

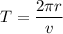
Circling frequency is given by :

`f=(1)/(T)=(v)/(2\pi r)`

`f=(2.42* 10^7)/(2\pi * 0.374 )`

`f=1.02* 10^7\ Hz`

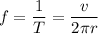
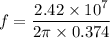
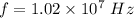
(d) The period of motion,

`T=(1)/(f)`

`T=(1)/(1.02* 10^7)`

`T=9.80* 10^(-8)\ s`