Question

The coordinate points of T are (0,6). The midpoint of ST is (6,-8). Find the coordinate of point S.

Answer 1

The coordinates of the point S = (12, -22)

Explanation:

The coordinate points of T = (0,6)

Mid point of ST = (6,-8)

Let the coordinates of S = (a,b)

Now, BY MID POINT FORMULA:

If (x, y) and (z, w) are the line point joining line segment and (p,q) is the coordinate of mid point. Then

`(p, q)  = ((x  + z)/(2)  , (y + w)/(2) )`

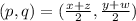
So, here similarly,
`(6, -8)  = (((0+a))/(2)  , (6+ b)/(2) )`

⇒
`6   = (0+a)/(2)  , -8 =  (6+ b)/(2)`

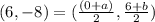
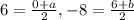
⇒ a =2 x 6 = 12, b = 2 (-8) -6 = -22

⇒(a,b) = (12, -22)

Hence, the coordinates of the point S = (12, -22)