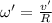Question

A disk-shaped merry-go-round of radius 2.93 m and mass 165 kg rotates freely with an angular speed of 0.691 rev/s . A 62.4 kg person running tangential to the rim of the merry-go-round at 3.11 m/s jumps onto its rim and holds on. Before jumping on the merry-go-round, the person was moving in the same direction as the merry-go-round's rim. Calculate the final kinetic energy for this system

Answer 1

The final kinetic energy of the system is 8.58 m/s

Solution:

As per the question:

Radius of merry-go-round, R = 2.93 m

Mass of merry-go-round, m = 165 kg

Angular speed,
`\omega = 0.691\ rev/s`

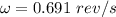
Velocity of the merry-go-around, v = 3.11 m/s

Mass of man, M = 62.4 kg

Now,

To calculate the moment of inertia of the merry-go-round:

`I_(M) = [tex](1)/(2)mR^(2)`

`I_(M) = [tex](1)/(2)* 165* (2.93)^(2) = 708.25\ kg.m^(2)`

`I = I_(M) + MR^(2) = 267.85 + 62.4* (2.93)^(2) = 1243.95\`

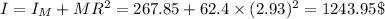
Initially, the angular momentum is given by:

`L = MvR + I_(m)\omega`

`L = 62.4* 3.11* 2.93 + 708.25* 0.691(2\pi \ rad/s)/(1\ rev/s) = 3643.60\ Js`

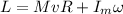
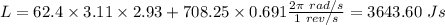
The final angular momentum is given by:

`L' = I\omega' = 1243.95\omega'`

where

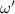`\omega'` = final angular velocity

Now, by conservation of momentum:

Initial momentum = Final momentum

`L' = L`

`1243.95\omega' = 3643.60`

`\omega' = 2.93\ rad/s`

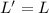
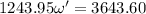
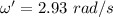
The final linear velocity, v' of the system:

`\omega' = (v')/(R)`

`v' = R\omega' = 2.93* 2.93 = 8.58\ m/s`

Answer 2

Step-by-step explanation:

The problem is related to rotational motion . So we shall find out rotational kinetic energy .

K E = 1/2 x I ω²

ω is the final angular velocity

Moment of inertial of the disk

I ₁ = 1/2 m r²

= .5 x 165 x 2.93²

= 708.25 kgm²

Moment of inertial of the person

I₂ = mr²

= 62.5 x 2.93²

= 536.55 kgm²

ω₂ = v / R

= 3.11 / 2.93 rad /s

At the time of jumping , law of conservation of angular momentum will apply

I₁ ω₁ + I₂ω₂ = (I₁ + I₂)ω

708.25 x0.691 + 536.55 x ( 3.11 / 2.93 ) = ( 708.25 + 536.55 ) ω

ω = 0 .85 rad/ s

K E = 1/2 x I ω²

= .5 x ( 708.25 + 536.55 ) ( .85 )²

449.68 J