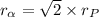Question

A proton (charge +e, mass mp), a deuteron (charge +e, mass 2mp), and an alpha particle (charge +2e, mass 4mp) are accelerated from rest through a common potential difference ?V. Each of the particles enters a uniform magnetic field B(-->) , with its velocity in a direction perpendicular to B(-->). The proton moves in a circular path of radius rp.

(a) In terms of rp, determine the radius rd of the circular orbit for the deuteron.
rd = _________



(b) In terms of rp, determine the radius r(aplha) for the alpha particle.

r(alpha)________________

Answer 1

(a)
`r_(d)=√(2)* r_(P)`

(b)
`r_(\alpha)=√(2)* r_(P)`

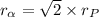
Step-by-step explanation:

charge on proton, q = e

mass pf proton, m = mp

charge on deuteron, q' = e

mass pf deuteron, m' = 2mp

charge on alpha particle, q'' = 2e

mass pf alpha particle, m'' = 4mp

Potential difference = V

Magnetic field = B

The kinetic energy is given by eV.

So, 1/2 mv^2 = e V

where, v be the velocity of the particle.

`v=\sqrt{(2eV)/(m)}`

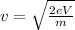
The formula for the radius of circular path is given by

`r = (mv)/(Bq)`

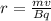
By substituting the value of v

`r = (√(2eVm))/(Bq)`

`r\alpha (√(m))/(q)`

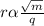
The radius of path of proton is given by

`r_(p)\alpha \frac{\sqrt{m_(p)}}{e}`.... (1)

(a) radius of deuteron

`r_(d)\alpha \frac{\sqrt{2m_(p)}}{e}`

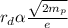
By comparing equation (1), we get

`r_(d)=√(2)* r_(P)`

(b) radius of alpha particle

`r_(\alpha)\alpha \frac{\sqrt{4m_(p)}}{2e}`

By comparing equation (1), we get

`r_(\alpha)=√(2)* r_(P)`