Question

A product is made up of components A, B, C, D, E, F, G, H, I, and J. Components A, B, C, and F have a 1/10,000 chance of failure during useful life. D, E, G, and H have a 3/10,000 chance of failure. Component I and J and a 5/10,000 chance of failure. What is the overall reliability of the product?

Answer 1

The overall reliability is 99.7402 %

Explanation:

The overall reliability of the product is calculated as the product of the working probability of the components.

For components A,B,C and F we have :

`P(failure)=(1)/(10000)`

⇒

`P(Work)=1-(1)/(10000)=(9999)/(10000)=0.9999`

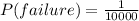
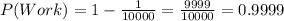
For components D,E,G and H we have :

`P(failure)=(3)/(10000)`

⇒

`P(Work)=1-(3)/(10000)=(9997)/(10000)=0.9997`

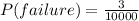
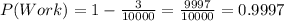
Finally, for components I and J :

`P(failure)=(5)/(10000)`

⇒

`P(Work)=1-(5)/(10000)=(9995)/(10000)=0.9995`

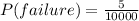
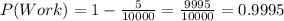
Now we multiply all the working probabilities. We mustn't forget that we have got ten components in this case :

Components A,B,C and F with a working probability of 0.9999

Components D,E,G and H with a working probability of 0.9997

Components I and J with a working probability of 0.9995

Overall reliability =
`(0.9999)^(4)(0.9997)^(4)(0.9995)^(2)=0.997402`

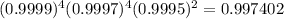
0.997402 = 99.7402 %