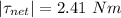Answer:
Magnitude the net torque about its axis of rotation is 2.41 Nm
Solution:
As per the question:
The radius of the wrapped rope around the drum, r = 1.33 m
Force applied to the right side of the drum, F = 4.35 N
The radius of the rope wrapped around the core, r' = 0.51 m
Force on the cylinder in the downward direction, F' = 6.62 N
Now, the magnitude of the net torque is given by:
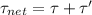
where
 = Torque due to Force, F
= Torque due to Force, F
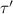 = Torque due to Force, F'
= Torque due to Force, F'
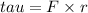
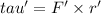
Now,

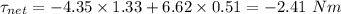
The net torque comes out to be negative, this shows that rotation of cylinder is in the clockwise direction from its stationary position.
Now, the magnitude of the net torque: