Question

A particle moves according to a law of motions=f(t),t≥0 Wheretismeasured in seconds andsin feet.a) Find the velocity at timet.b) When is the particle at rest.c) When is the particle moving in the positive direction.d) Find the total distance traveled during the first 6 seconds.e) When is the particle speeding up? When is it slowing down? 9t/(t^2+9)

Answer 1

a)
`v(t) = (9)/(t^2+9) - (18t^2)/((t^2+9)^2)`

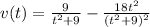
b) 3s

c) t < 3s

d) 1.8ft

e) particle is speeding up when t > 5.385 s and vice versa, slowing down when t < 5.385 s

Step-by-step explanation:

a)Suppose the equation for motion is:

`f(t) = (9t)/(t^2+9)`

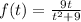
Then the velocity is the derivative of the motion function

`v(t) = (df(t))/(dt) = (9t(t^2+9)^(-1))^'`

From here we can apply product rule

`v(t) = (9t)^(')(t^2+9)^(-1) + (9t)((t^2+9)^(-1))^'`

`v(t) = (9)/(t^2+9) - (9t(2t))/((t^2+9)^2)`

`v(t) = (9)/(t^2+9) - (18t^2)/((t^2+9)^2)`

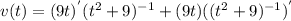
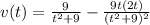
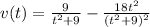
b) The particle is at rest when v(t) = 0:

`(9)/(t^2+9) - (18t^2)/((t^2+9)^2) = 0`

`(9)/(t^2+9) = (18t^2)/((t^2+9)^2)`

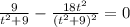
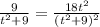
Multiply 2 sides by
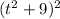`(t^2+9)^2` we have:

`t^2 + 9 = 2t^2`

`t^2 = 9`

`t = 3s`

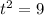
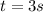
(c) The particle is moving in positive direction when v(t) > 0:

`(9)/(t^2+9) - (18t^2)/((t^2+9)^2) > 0`

`(9)/(t^2+9) > (18t^2)/((t^2+9)^2)`

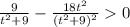
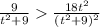
Multiply 2 sides by
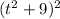`(t^2+9)^2` we have:

`t^2 + 9 > 2t^2`

`t^2 < 9`

`t < 3s`

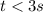
(d) As particle is moving in positive direction when t < 3s and negative direction when t > 3s, we can calculate the distance it's moving up to 3s and then after 3s

`f(3) = (9*3)/(3^2+9) = (27)/(18) = 1.5 ft`

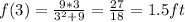
At 3s, particle is changing direction to negative, so its position at 6s is

`f(6) = (9*6)/(6^2+9) = (54)/(45) = 1.2 ft`

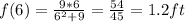
Therefore from 3s to 6s it would have moved a distance of 1.5 - 1.2 = 0.3 ft

Then the total distance it has moved in the first 6 s is 1.5 + 0.3 = 1.8 ft

e) Acceleration is the derivative of velocity function:

`a(t) = (dv(t))/(dt) = ((9)/(t^2+9) - (18t^2)/((t^2+9)^2))^'`

`a(t) = -(9(2(t^2+9))(2t))/((t^2+9)^2) - (36t)/((t^2+9)^2) + (18t^2(2(t^2+9))(2t))/((t^2+9)^3)`

`a(t) = -(36t)/(t^2+9) - (36t)/((t^2+9)^2) + (72t^3)/((t^2+9)^2)`

`a(t) = -(54t)/(t^2+9) + (72t^3 - 36t)/((t^2+9)^2)`

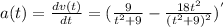
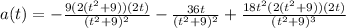
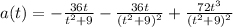
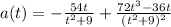
Particle is speeding up when a(t) > 0:

`-(54t)/(t^2+9) + (72t^3 - 36t)/((t^2+9)^2) > 0`

`(72t^3 - 36t)/((t^2+9)^2) > (54t)/(t^2+9)`

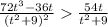
as
`t \& (t^2 + 9)^2 \geq 0` we can multiply/divide both sides by it:

`8t^2 - 4 > 6(t^2+9)`

`8t^2 > 6t^2 + 58`

`t^2 > 29`

`t > \sqrt(29) \approx 5.385 s`

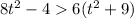
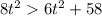
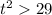
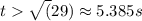
so particle is speeding up when t > 5.385 s and vice versa, slowing down when t < 5.385 s