Question

A pipe with cross-sectional area 2.0 m^2 is joined to a second pipe with cross-sectional area 0.5 m^2. The pipes are both completely filled with water. The water in the 2.0 m^2 pipe is flowing into the smaller pipe with a speed of 2 m/s. How fast is the water flowing in the second pipe?

a.) 8 m/s

b.) 0 m/s

c.) 4 m/s

d.) 2 m/s

Answer 1

a.) 8 m/s

Step-by-step explanation:

Given that

A₁= 2 m²

V₁= 2 m/s

A₂=0.5 m²

Lets take speed in 0.5m² is V₂

As given that both pipes are connected in the series that is volume flow rate will be same

Q= A₁V₁ = A₂V₂

Now by putting the values

A₁V₁ = A₂V₂

2 x 2 = 0.5 x V₂

V₂= 8 m/s

a.) 8 m/s

Answer 2

`v_2=8\ m/s`

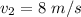
Step-by-step explanation:

It is given that,

Area of cross section of the pipe,
`A_1=2\ m^2`

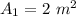
Area of cross section of the another pipe,
`A_2=0.5\ m^2`

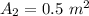
Speed of water in first pipe,
`v_1=2\ m/s`

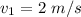
To find,

Speed of the water flowing in the second pipe.

Solve,

Let
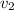`v_2` is the speed of water flowing in the second pipe. The relation between the area of cross section and the velocity is given by the continuity equation. It is given by :

`A_1v_1=A_2v_2`

`v_2=(A_1v_1)/(A_2)`

`v_2=(2* 2)/(0.5)`

`v_2=8\ m/s`

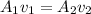
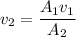
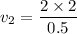
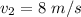
Therefore, the water is flowing in the second pipe at the rate of 8 m/s.